Ice-crystal fabric
Introduction
Glacier ice is composed of small grains that grow in size with depth, starting at the millimeter scale at the surface and growing to centimeters or more deep in the ice sheet. At the surface, these crystals are randomly oriented, because snow falls in random orientations. Deeper in a glacier, deformation causes these crystals to tend to align in preferred direction, which has some interesting effects.
It is easiest to start by thinking of an individual ice crystal. Each ice crystal has its water molecules bonded in a hexagonal crystal lattice–this lattice is quasi-rotationally symmetric in its hexagonal plane (think of a snow flake–if you rotate it by 60 degrees it looks the same). However, the direction perpendicular to this hexagonal plane does not match this symmetry, and we term this direction the c-axis. We can then describe an individual crystal based on its c-axis orientation. This orientation is a result of the flow history of that crystal–how it pointed when it fell as snow, how it was squashed, stretched, and rotated with ice flow. This ice crystal fabric affects deformation by making it easier in some directions (think of a deck of cards–two directions of deforming the deck are easy, one is hard).
Goals
Ice-crystal fabric causes mechanical anisotropy in ice–that is to say, depending on the orientation of the ice crystals, ice flow is easier or harder. Incorporating the effect of this mechanical anisotropy is a key way to make models of ice flow more accurate. Better understanding the effect of fabric on ice flow is the main goal of my fabric-related work.
Since ice crystals are reoriented by flow, they may also lend us information about how ice flowed in the past. Since we only have a relatively short time series of observations of ice flow, inferring ice flow over long periods using fabric could be very useful to contextualize modern ice-sheet retreat. Developing the methods to use ice-crystal fabric as such a proxy is a secondary goal of my fabric work.
Fabric basics
Thinking about what happens to an individual crystal is well and good, but if we want to understand how a whole glacier moves we are thinking about an enormous number of crystals, far too many for us to keep track of individually. Instead, we think of a “crystal fabric”, some kind of aggregate of grains that we may be able to describe in relatively simple mathematical terms. Isotropic (randomly oriented), girdle (forming a circle) and single maximum (pointing mainly in one direction) are probably the most common fabric types in ice.
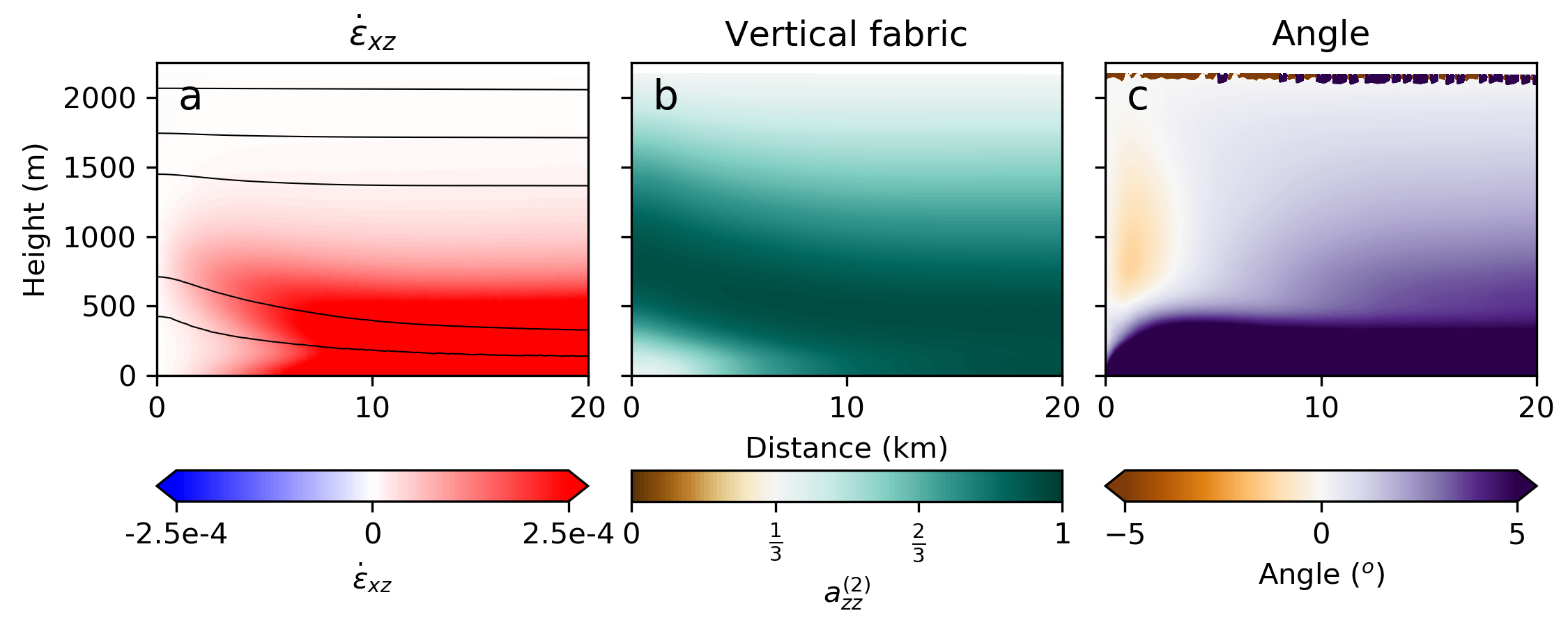
Ice divides (ice flows vertically and in one horizontal dimension away from a ridge), or domes (ice flows radially outward from the dome center), are the simplest to think about since the flow fields in these areas are relatively tame. I’ll focus on divides. At divides, the surface has no slope, so there is no shear stress but only downward stress due to gravity, extensional stress away from the divide, and some containing force along the divide. At the divide, the crystal fabric gradually transitions from isotropic (randomly oriented) at the surface to a girdle, or circle in the plane of the divide, due to the extensional stresses. At depth, the ice reaches something of single maximum with crystals pointing upwards, where the vertical stresses dominate. This type of fabric has been seen in ice cores, and models can do a reasonable job reproducing it (see figure below). Just off the divide, we get complex effects as ice is moved around and stress states become more complex. This is seen, for example, in the angle of the fabric which tends to point leftward at certain depths in the right panel of the figure, or in the complex pattern of the shear strain in the left panel. Fabrics are not entirely intuitive, and assessing what fabrics are likely to result from complex deformation regimes is best done with an ice-flow model.
Effect on flow
Recently we worked on methods to infer fabric from radar, providing a small update to the 15-year old methodology that is widely used. Applying multiple methods to radar data from the Northeast Greenland Ice Stream (NEGIS) has shown that fabric there significantly affects flow. Moreover, we have shown that recent, slow speedup of NEGIS is likely due to fabric development.
Modeling
In an ice flow model, we seek to approximate how fabric evolves in response to the deformation of ice, and how it affects the deformation of the glacier. Modeling ice-crystal fabric is a fairly difficult exercise: the fabric evolves in multiple dimensions, it get moves around by ice flow, and the description we use is continuous despite the fabric itself being discrete. I have been helping Nicholas Rathmann with his work developing a new, small-scale model of ice flow. This work has allowed us to demonstrate that, even though most of us would love to avoid the complications of fabric, fabric really is important for understanding ice-flow properties that people care about, like basal conditions. We have also worked to improve how the modeled fabric is coupled to flow. With these developments in hand, I recently submitted a paper implementing Nicholas’ model in Elmer/Ice; this allowed recrystallization, an important and often-neglected fabric process, to be included, and makes the model applicable to a wider range of areas. Elmer/Ice has a relatively large user base, so hopefully this work helps others out as well!
Inferring flow history
To see if we could infer flow history from fabric, I ran a number of model simulations along flowtubes. This work was published in 2021. The model was implemented in Elmer/Ice, an open-source software package that is one of the only codes capable of handling the coupled evolution of ice flow and fabric. Using the model, we can get a sense of what fabrics result from ice streams, shown here for a few different ways of having the ice converge together to form a stream.
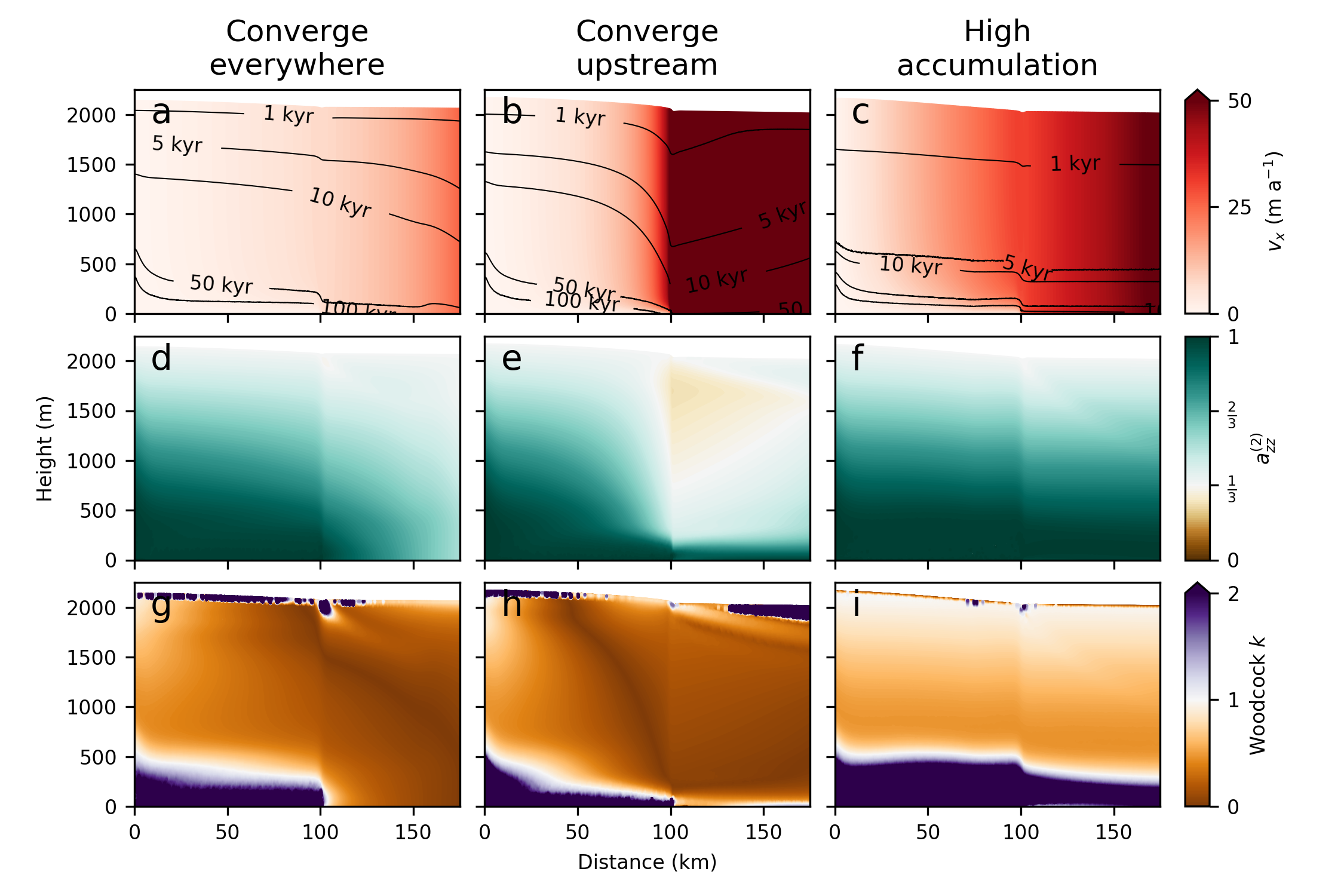
Anisotropic modeling of ice streams. Details are not critical here, but these fabrics are readily distinguished from non-streaming flow.
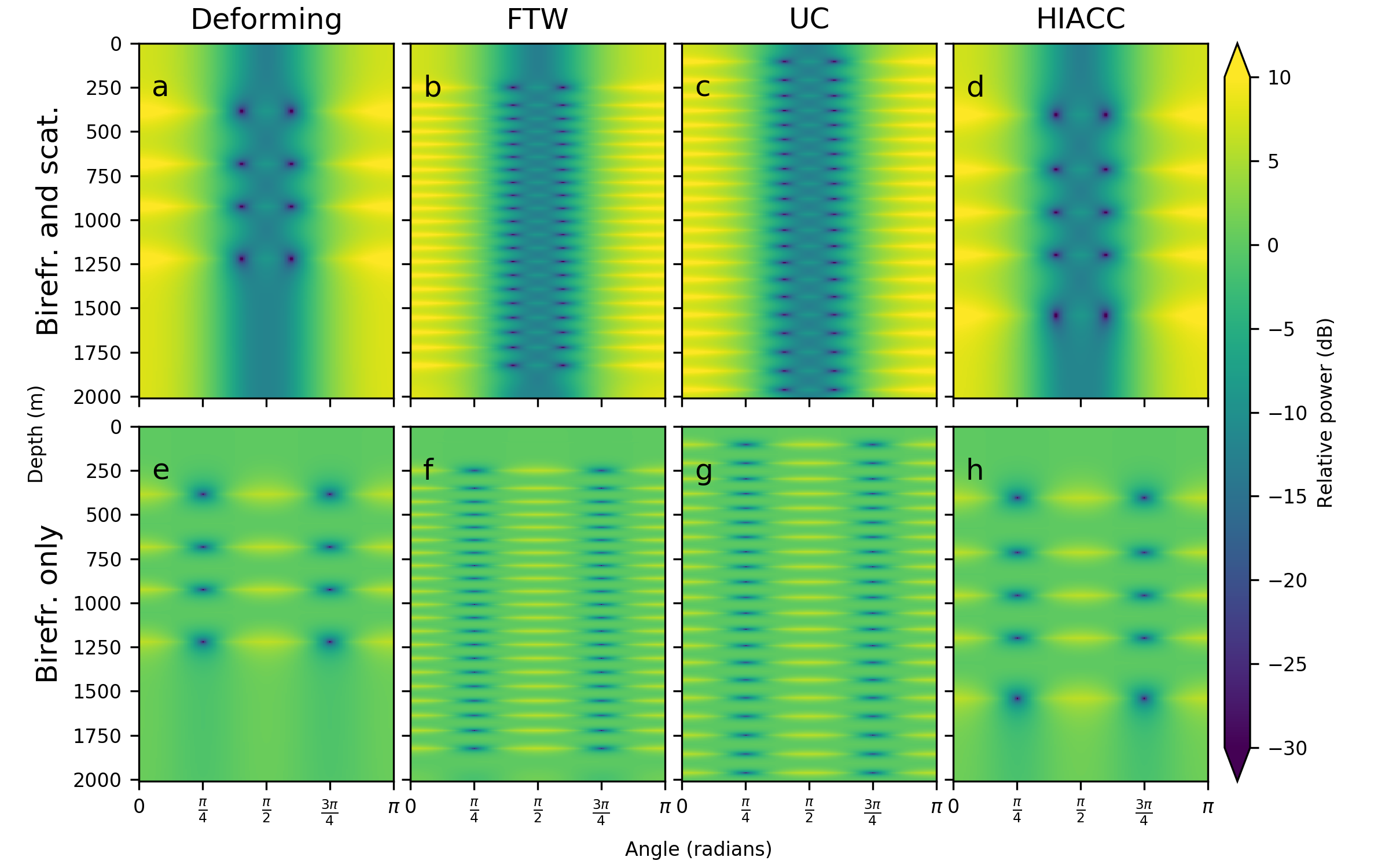
Skipping over the details of all the simulations I have run, it is important to ask whether we could observe these differences. Ice cores allow quite detailed measurement of fabric, so it is almost given that they could resolve these fabrics. However, it would be particularly exciting if we could observe the fabrics without drilling. One potential tool for this is pRES or ApRES, a type of phase sensitive radar. By rotating the radar around, we can identify some integrated information about the fabric. I have used the output of the ice-flow model to generate synthetic radargrams, which tell us what to expect when observing such fabrics with pRES in the field. As seen in the figure below, these are quite complicated, but easily distinguished from pure internal deformation (on the left). This is quite encouraging, and suggest that it should be possible to identify changes to past ice-stream flow by observing the fabric from the surface.
So how can all this information be used to infer past ice flow? It takes a relatively long time to reorient the ice crystals (thousands of years or more), so if modern ice-crystal fabric does not match modern ice flow, we may have evidence of past changes. Moreover, if we can use an ice-flow model to match different changes to flow with different fabrics, we may be able to identify what changes could cause such a mismatch between fabric and flow. I have been working to model how changes to ice streams will be manifest in the crystal fabric, and thus what we might look for in terms of inferring past changes.